Iterative Bayesian filtering and adaptive sampling for uncertainty quantification
|
Adaptive multi-level resampling using a Dirichlet process Gaussian mixture
|
An iterative Bayesian filtering framework for fast and automated calibration of DEM models
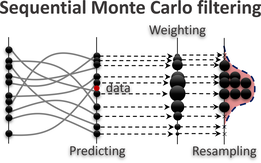
The novelty of the iterative Bayesian filter consists in recursively updating the posterior distribution of model parameters in time and iterating the process with new samples drawn from a proposal density. Over iterations, the proposal density is progressively localized near the posterior modes. The Dirichlet process Gaussian mixture is trained for estimating the proposal density from sparse and high dimensional data. As an example, the posterior distribution of the micromechanical parameters, conditioned on the experimentally measured stress-strain behavior of a granular assembly, is approximated.
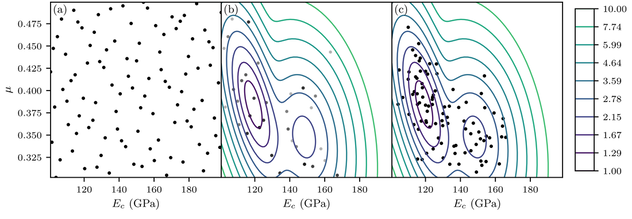
With the previously approximated posterior chosen as the new proposal density, the model evaluations are limited to those within highly probable parameter subspaces. As new result, the proposed framework provides a deeper understanding of the correlations between the uncertainty of the micromechanical parameters and the macroscopic quantities of interest, conditioned on the experimental data. Therefore, the iterative Bayesian filtering framework has a great potential for quantifying uncertainties and their propagation across various scales in granular materials.
With the previously approximated posterior chosen as the new proposal density, the model evaluations are limited to those within highly probable parameter subspaces. As new result, the proposed framework provides a deeper understanding of the correlations between the uncertainty of the micromechanical parameters and the macroscopic quantities of interest, conditioned on the experimental data. Therefore, the iterative Bayesian filtering framework has a great potential for quantifying uncertainties and their propagation across various scales in granular materials.
Evolution of the posterior distribution of micro-parameters over an oedometric stress history
|
1st iteration
3rd iteration
|
2nd iteration
4th iteration
|
