Main research interests
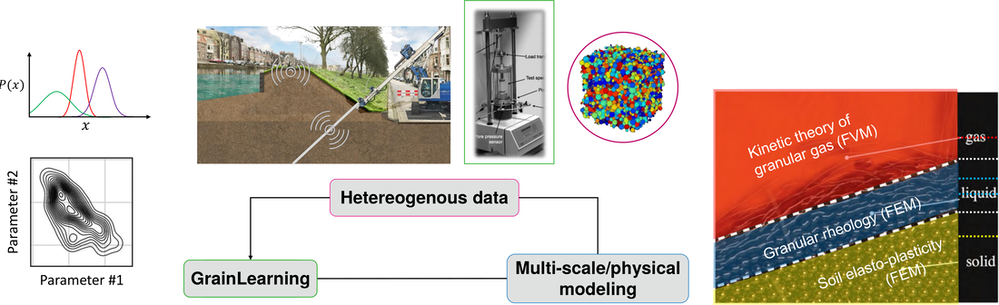
Granular materials are ubiquitous in nature but remain rather difficult to model accurately. Existing models only work for a specific (fluid, solid, and gas) state and are scattered in different disciplines, including geotechnics, fluid mechanics, physics, etc. I am interested in the mechanics and multi-scale/physical modeling of granular materials in processes where the interplay between the mechanics and physics at various scales is important. My research focuses on establishing the links between predictive models of granular materials, at different scales, and their observation data, via
- efficient coupling of the numerical tools (e.g., multi-scale and hydro-mechanical)
- and model-model or model-data integration using statistical inference and machine learning tools.
The goal is to develop computational-statistical tools towards Integrated Computational Materials & Engineering (ICME) to advance the understanding and modeling of granular materials in all physical states, as well as their transitions. To this end, I have been focusing on the development of open-source tools for multi-scale and multi-phase/physics modeling, Bayesian inference, and microscopic observation, and applied them to
- investigate geosynthetic/fiber-soil interactions
- develop constitutive models of granular soils based on a parameter-driven approach
- understand (nonlinear) wave propagation in dry and saturated granular media
- virtual prototype powder bed fusion processes